重点摘要

写二分查找的心法是：

维护low是我们要找的那个位置。high可以大胆地缩小目标空间。终结条件是：low > high，也就是目标空间为空。这时，low就是我们要找的点。

标准二分查找问题

标准二分查找的要求如下（假设表中没有重复的数字）：

1. 如果表中存在目标数，返回目标数在表中的下标。
2. 如果表中不存在目标数，返回表中小于目标数的元素的数量。（和返回元素应该插入的位置是一回事）

二分法思路很简单：

每次都和中位数比较大小，如果目标数大于中位数，则丢弃所有中位数之前的数字（包括中位数）。反之，则丢弃中位数和其之后的所有数字。

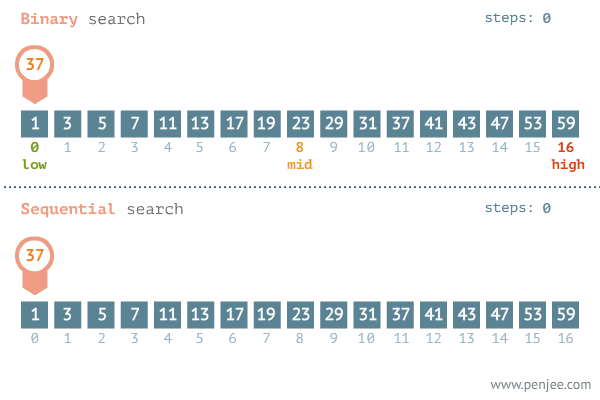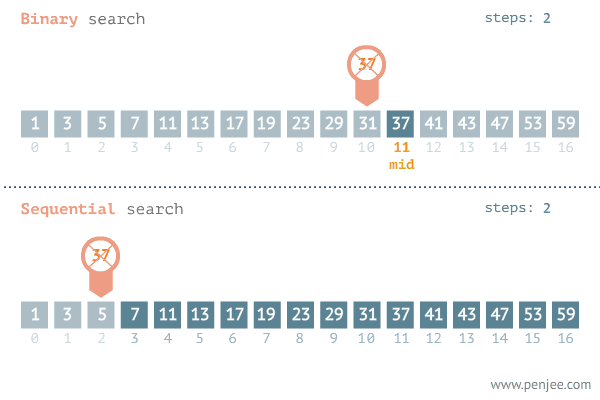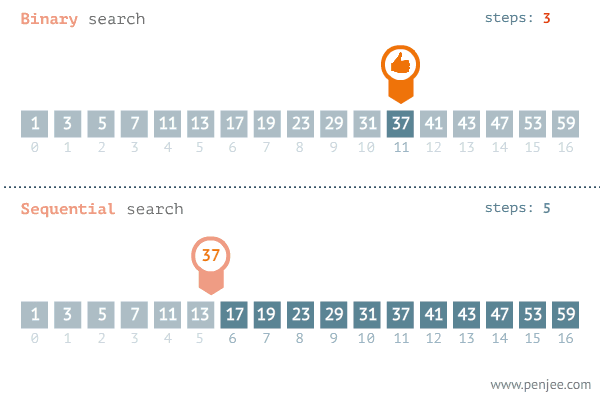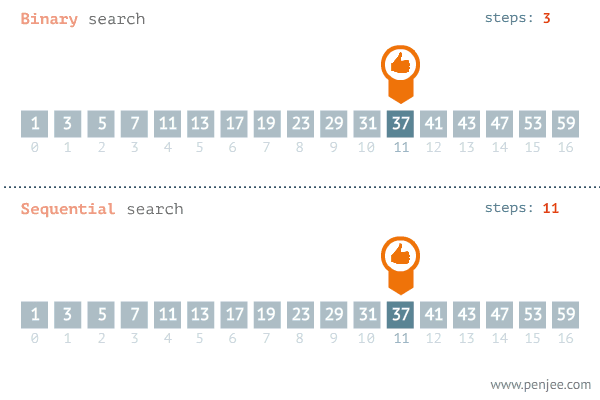
先要搞清楚几个重要的数字

首先说明，这里使用的是两头都包含的下标[low,high]。即low指向首元素，high指向尾元素。当然使用半开半闭空间[low,high)或者(low,high]，或者两头都不包含的空间都是可以的。但没必要每种情况都去试。只需要保持一种自己习惯的用法就好。我比较喜欢两头都包含。

对于任意一个有序互异数组，

• 初始最小下标：low = 0
• 初始最大下标：high = length - 1
• 数组长度：length = high - low + 1
• 如果数组长度是奇数：
  • 中位数：median = (length - 1) / 2
• 如果数组长度是偶数：
  • 下位中位数：lowerMedian = (length - 2) / 2
  • 上位中位数：upperMedian = length / 2
• 不论数组长度是奇数还是偶数，下位中位数的一般表达式为：
  • median = floor((length - 1) / 2) (向下取整)

Java的整数除法自动向下取整，所以中位数可以用下面公式表达。>> 1右位移一位，表示/ 2。

int median = low + ( (high - low) » 1 )

这里有个常见的坑，不要用int median = (low + high) / 2，缺点是low + high有可能超过int的最大值，造成溢出。

最后，以下面这个数组为例，

[2,3,4,7,8,9]

首元素2的下标为0。末尾元素9的下标为5。数组长度为：5-0+1 = 6。下位中位数4的下标为：0+(5-0)/2 = 2。

关于终结条件的细节

虽然二分法的思想很简单，但终结条件的选择需要仔细思考。尤其是数组长度为1或者2这样的极限条件。

以low == high作为终结条件在这里不适用

如果不深入思考，最容易想到的是以low == high作为终结条件。

if (low == high) {
    return (nums[low] >= target)? low : ++low;
}

但这样没有覆盖到所有情况。例如下面这个例子，指针会跳过low == high的阶段，两个指针直接交叉low > high。

最开始low = 0，high = 1，median = 0。当比较了一次nums[0] > target之后，high指针会直接变成high = -1。没有经过low == high的终结条件。

但这不代表low == high永远不能作为终结条件。还是需要具体问题具体分析。关键在于要仔细推演长度为1或者2的各种可能情况。

如果要用low == high作为终结条件，代码可以是这样的，

if (low >= high) { //也算上直接交叉的情况
    return (nums[low] >= target)? low : ++low;
}

应该以low > high为终结条件，并返回low

如下图所示，

任何一种情况，都只要返回low下标即可。这是对终结条件的一种高度归纳。

仔细观察low下标的行为，

它的初始值为0，而且只有在确定目标数大于某个位置元素之后，low才前移到这个位置的下一位，而且永远不会变小。

所以low指针最终指向的位置就是我们要找的小于目标数的元素的数量，或者换一种说法，目标元素的位置，或者应该插入的位置。

但也需要注意，未必是所有二分查找的变种都能归纳到low > high程度。还是一句话，

需要具体问题具体分析。关键在于要仔细推演长度为1或者2的各种可能情况。

标准二分查找代码

标准二分查找的要求如下（假设表中没有重复的数字）：

1. 如果表中存在目标数，返回目标数在表中的下标。
2. 如果表中不存在目标数，返回表中小于目标数的元素的数量。（和返回元素应该插入的位置是一回事）

迭代版

public int binarySearch(int[] nums, int target) {
    int low = 0, high = nums.length-1;
    while (low <= high) { // 注意是 <=。 所以==的情况不是终结条件。low>high交叉了才是。
        int mid = low + ( (high - low) >> 1 );
        if (nums[mid] < target) { low = mid + 1; }
        if (nums[mid] > target) { high = mid - 1; }
        if (nums[mid] == target) { return mid; }
    }
    return low;
}

递归版

public int binarySearchRecur(int[] nums, int target, int low, int high) {
    if (low > high) { return low; } //base case
    int mid = low + ( (high - low) >> 1 );
    if (nums[mid] > target) {
        return binarySearchRecur(nums,target,low,mid-1);
    }  else if (nums[mid] < target) {
        return binarySearchRecur(nums,target,mid+1,high);
    } else {
        return mid;
    }
}

简化的二分查找

简化的二分查找的要求如下（假设表中没有重复的数字）：

1. 如果表中存在目标数，返回目标数在表中的下标。
2. 如果表中不存在目标数，返回-1。

终结条件同样是low > high。因为low > high的时候，数组空间为空，代表不可能再找到了。而且不需要纠结返回值的问题。因为找不到直接返回-1。

迭代版

public int simpleBinarySearch(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    while(low <= high) { // 终结条件：low > high。空间里候选数字为空。找不到了。
        int mid = low + ( (high - low) >> 1 );
        if (nums[mid] < target) { low = mid + 1; }
        if (nums[mid] > target) { high = mid - 1; }
        if (nums[mid] == target) { return mid; }
    }
    return -1;
}

递归版

public int simpleBinarySearchRecur(int[] nums, int target, int low, int high) {
    if (low > high) { return -1; }
    int mid = low + ( (high - low) >> 1 );
    if (nums[mid] < target) {
        return simpleBinarySearchRecur(nums,target,mid+1,high);
    } else if (nums[mid] > target) {
        return simpleBinarySearchRecur(nums,target,low,mid-1);
    } else {
        return mid;
    }
}

有重复数字的二分查找：查找某元素第一次出现的位置，或者第一个大于等于目标数的元素位置

具体要求如下：

1. 表中可以有重复的数字
2. 如果表中存在目标数，返回目标数在表中第一次出现位置的下标。
3. 如果表中不存在目标数，返回目标数应该插入位置的下标。

该问题也可以表述为：第一个大于等于目标数的元素位置。C++的STL中有对应的库函数 lower_bound()。

本质上，这是标准二分查找的一个推广。是更广义的二分查找，同样可以作用于没有重复数字的标准二分查找。

可以借鉴标准二分查找的思路：维护low。主要逻辑有两条：

1. low从0起始，只在mid遇到确定小于target的数时才前进，并且永不后退。low就是我们要的那个点。所以，最后可以直接返回low。
2. high可以大胆地缩小目标空间。在mid遇到大于或等于target的数时都往回退，而且跳过mid。因为就算跳过的就是要找的那个位置，low最后也会到这个位置。

举个例子，有如下数组，找数字9，

[7,7,7,7,>9<,10,10,10,11,12]

第一次取中值，就命中了9。但high可以大胆地跳过9，跑到最后一个7的位置。因为到最后，low还是会跑到9这个位置。

迭代版代码

public int firstOccurrence(int[] nums, int target) {
    int low = 0, high = nums.length-1;
    while (low <= high) {
        int mid = low + ( (high - low) >> 1 );
        if (nums[mid] < target) { low = mid + 1; }
        if (nums[mid] >= target) { high = mid - 1; }
    }
    return low;
}

递归版代码

public int firstOccurrenceRecur(int[] nums, int target, int low, int high) {
    if (low > high) { return low; }
    int mid = low + ( (high - low) >> 1 );
    if (nums[mid] < target) {
        return firstOccurrenceRecur(nums,target,mid + 1,high);
    } else {
        return firstOccurrenceRecur(nums,target,low,mid-1);
    }
}