题目

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example:
Input: "babad"
Output: "bab"
Note: “aba” is also a valid answer. Example:
Input: "cbbd"
Output: "bb"
暴力遍历所有子串,复杂度O(n^3)
最暴力的解法,就是遍历字符串的所有子串,并判断每个子串是否为对称回文。因为字符串所有子串的复杂度为O(n^2),再判断回文,总体复杂度达到O(n^3)。
下面我这个版本做了一些优化,
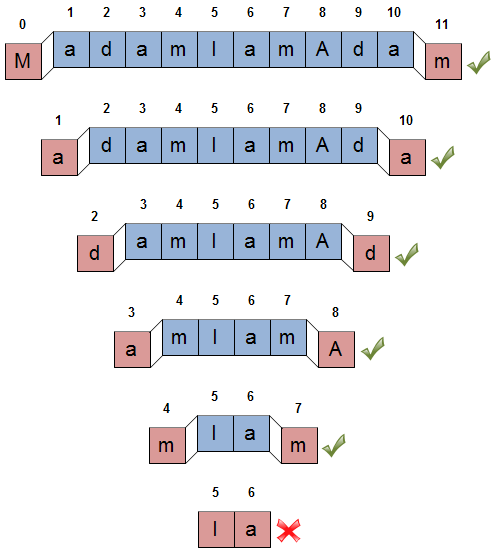
从最长的子串开始遍历,一旦找到一个回文,就终止迭代。 判断回文采用收缩法。从最外一对字符往中心推进。大部分子串在一开始就会迅速失败。
代码
public class Solution {
public String longestPalindrome(String s) {
for (int size = s.length(); size > 0; size--) {
for (int low = 0, high = low+size-1; high < s.length(); low++, high++) {
if (shrinkCheckPalindrome(s,low,high)) {
return s.substring(low,high+1);
}
}
}
return s.substring(0,1);
}
public boolean shrinkCheckPalindrome(String s, int low, int high) {
while (low <= high) {
if (s.charAt(low) == s.charAt(high)) {
low++;
high--;
} else {
return false;
}
}
return true;
}
}
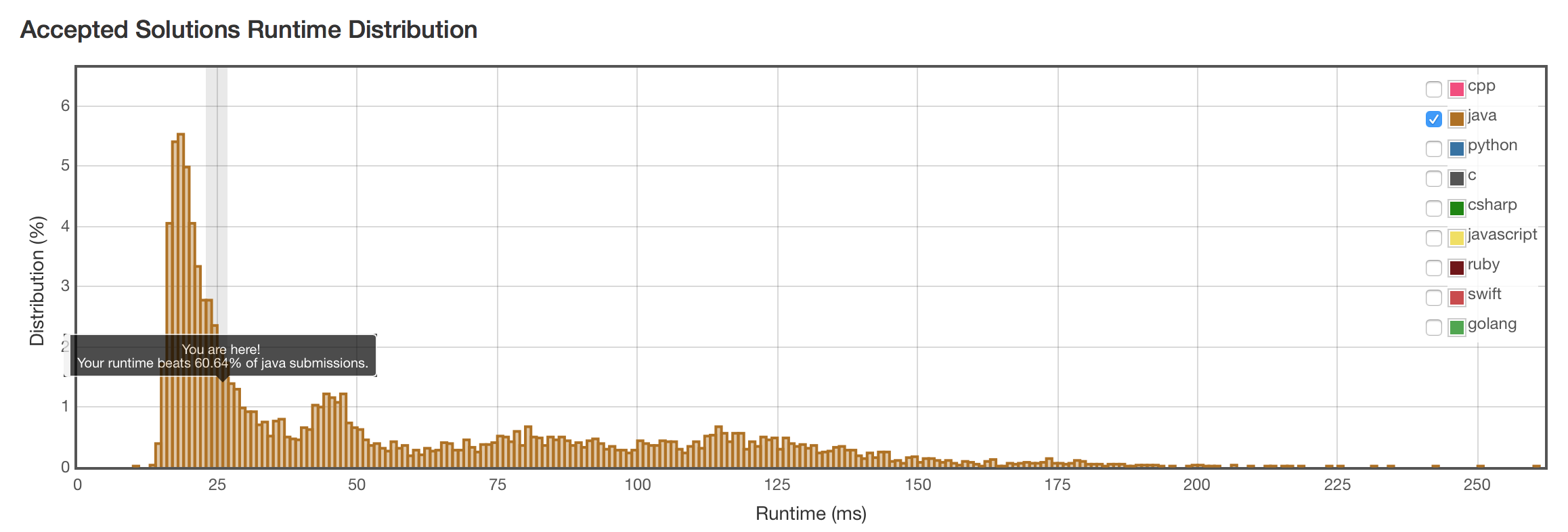
结果
实际运行的复杂度是没有O(n^3)这么恐怖。结果将将通过。
从中心点向外扩散,复杂度O(n^2)
回文就是中心对称的单词。从字符的中心开始,向两边扩散检查回文。这需要从头开始,以每一个位置为中心遍历一遍。注意,回文需要同时检查单核aba以及双核abba的情况。复杂度为O(n^2)。
代码
public class Solution {
private int max = 0;
private String res = "";
public String longestPalindrome(String s) {
if (s.length() == 1) { return s; }
for (int i = 0; i < s.length()-1; i++) {
checkPalindromeExpand(s,i,i);
checkPalindromeExpand(s,i,i+1);
}
return res;
}
public void checkPalindromeExpand(String s, int low, int high) {
while (low >= 0 && high < s.length()) {
if (s.charAt(low) == s.charAt(high)) {
if (high - low + 1 > max) {
max = high - low + 1;
res = s.substring(low,high+1);
}
low--; high++;
} else {
return;
}
}
}
}
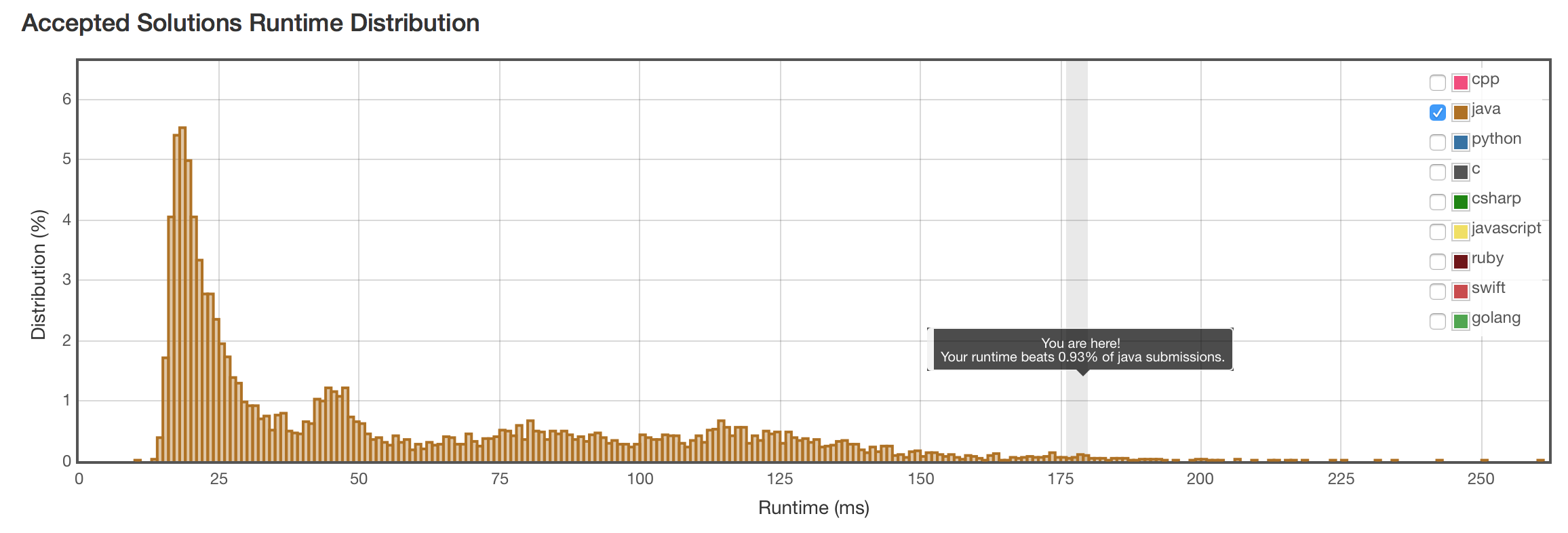
结果
速度比遍历所有子字符串的方法快了一倍。
Manacher算法,复杂度O(n)
Manacher算法是计算最长回文子串的最理想方法。实际上中心点扩散法还是有一些字符是重复判断了。Manacher算法正是在刚才的中心点扩散法的基础上,做了优化,跳过了某些点的判断工作,因为根据之前判断过的内容,可以推断出后面字符的对称情况。
第一种可以跳过的情况
如下图所示,
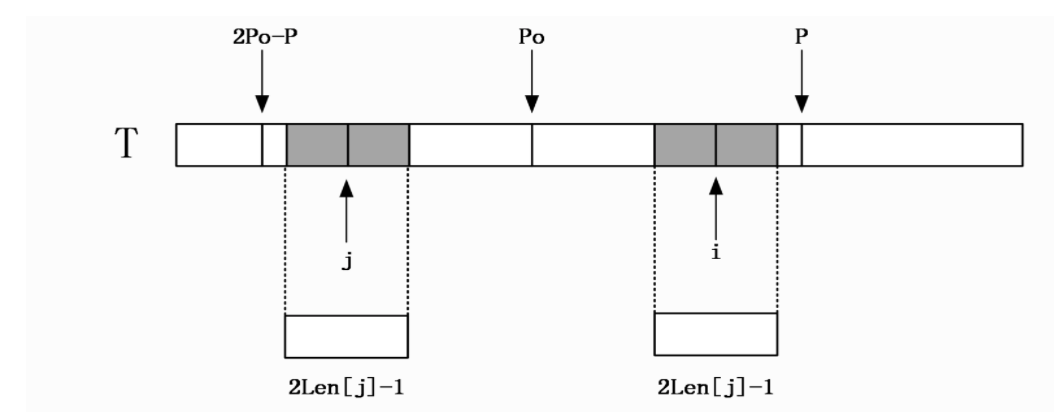
当前面的某次扩散检查已经找到以Po为中心,以P为边界的回文。那么另一边的镜像边界就可以算出来,是2Po-P。假设我们向前推进,以i为中心,向外扩散检查回文。
当i点处在P边界之内的时候,我们是有机会推算出i点的对称回文长度的。因为2Po-P-Po-P这一段回文是沿着中心点Po对称的。我们可以找出i点关于Po中心的镜像点j,它的下标是2Po-i。以j为中心的对称回文长度,前面已经检查过了,如果我们用动态规划,把这个信息保存起来的话,这时候就可以取出来。重点来了,如果以j为中心的对称回文长度没有超过另一边端点2Po-P覆盖范围的话,我们就可以断定以i为中心的最长回文也不会超过Po端点。因为2Po-P-Po-P是回文,是对称的。
既然回文长度已经算出来了,就不需要再扩展检查了。
第二种可以跳过的情况
如下图所示,
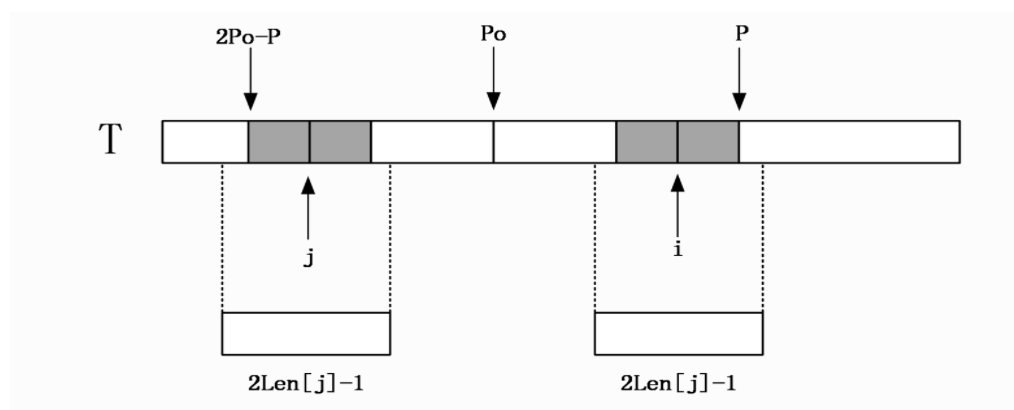 当我们找到
当我们找到j点的历史记录,发现j点的回文长度超过了2Po-P端点的覆盖范围,根据对称性,我们只能断定以i点为中心的最长回文至少会延伸到P端点的位置。至于再往下还是不是回文,还是需要老老实实逐个检验的。但至少我们可以直接跳到P点的下一个元素再往下检查。这也省了一部分力。
不可跳过的情况
如下图所示,
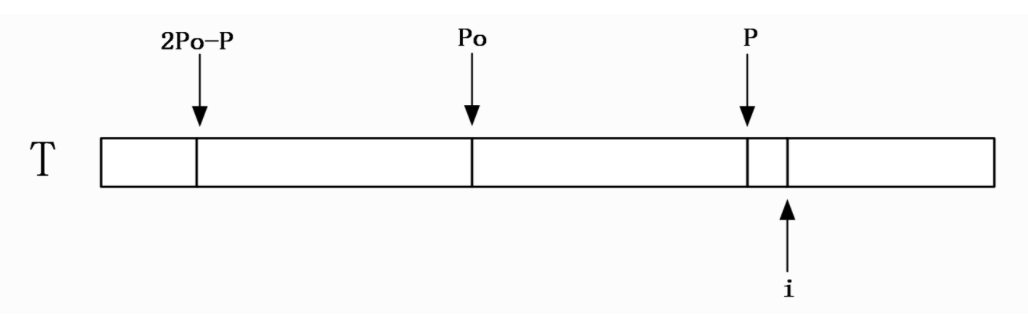 如果
如果i点的位置,没有被之前任何一段回文覆盖,我们就只能老老实实一个一个字符往下验证。
复杂度
仔细观察,根据前面两种可以跳过的情况,可以发现,验证元素对称性的指针是不会回退的。只要前面某次回文检查扩散到P点位置了,接下来所有以后续元素为中心点的回文检查,都至少可以从P的位置开始验证(第二种情况)。如果运气好,遇到第一种情况,验证步骤直接省去,因为回文长度已经算出来了。所以Manacher算法只遍历一遍字符串,从不回头,所以复杂度是O(n)。
代码
实现的时候,为了避免单核aba和双核abba的区别,先要在字符串的中间都插入特殊字符。为了避免下标溢出,首尾都加上一个节点。
// 处理前
abba
// 处理后
$#a#b#b#a#@
下面是Sedgewick的《算法》练习中附带的Manacher算法的Java实现。
public class Solution {
private int[] p; // p[i] = length of longest palindromic substring of t, centered at i
private String s; // original string
private char[] t; // transformed string
// longest palindromic substring
public String longestPalindrome(String str) {
s = str;
preprocess();
p = new int[t.length];
int mid = 0, right = 0;
for (int i = 1; i < t.length-1; i++) {
int mirror = 2*mid - i;
if (right > i)
p[i] = Math.min(right - i, p[mirror]);
// attempt to expand palindrome centered at i
while (t[i + (1 + p[i])] == t[i - (1 + p[i])])
p[i]++;
// if palindrome centered at i expands past right,
// adjust center based on expanded palindrome.
if (i + p[i] > right) {
mid = i;
right = i + p[i];
}
}
int length = 0; // length of longest palindromic substring
int center = 0; // center of longest palindromic substring
for (int i = 1; i < p.length-1; i++) {
if (p[i] > length) {
length = p[i];
center = i;
}
}
return s.substring((center - 1 - length) / 2, (center - 1 + length) / 2);
}
// Transform s into t.
// For example, if s = "abba", then t = "$#a#b#b#a#@"
// the # are interleaved to avoid even/odd-length palindromes uniformly
// $ and @ are prepended and appended to each end to avoid bounds checking
private void preprocess() {
t = new char[s.length()*2 + 3];
t[0] = '$';
t[s.length()*2 + 2] = '@';
for (int i = 0; i < s.length(); i++) {
t[2*i + 1] = '#';
t[2*i + 2] = s.charAt(i);
}
t[s.length()*2 + 1] = '#';
}
}
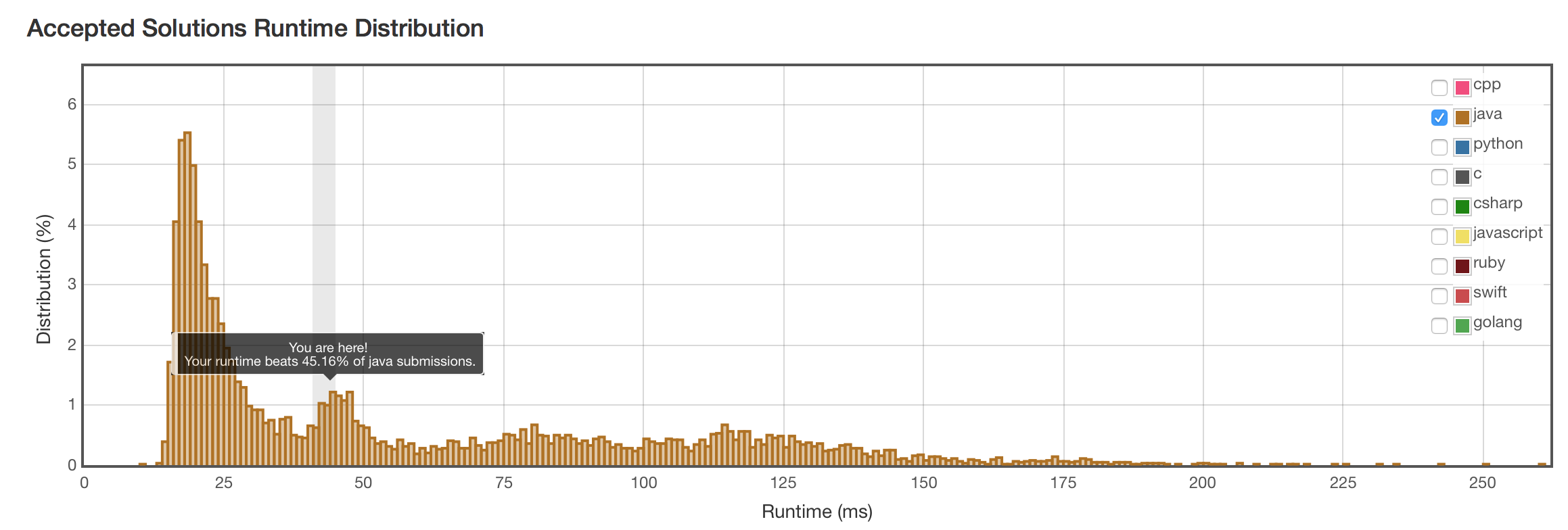
结果
25ms,又快了一倍。