Leetcode - Algorithm - Letter combination of a phone number

    |     algorithm leetcode backtracking string   |    

主要收获

n叉树的遍历，用递归非常简洁！

题目

Given a digit string, return all possible letter combinations that the number could represent. A mapping of digit to letters (just like on the telephone buttons) is given below. phone-keypad

Input:Digit string "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

Note: Although the above answer is in lexicographical order, your answer could be in any order you want.

迭代回溯算法 \(O(3^n)\)

记录一个键盘数字和字母的映射表。组合字母的时候，遍历现有字符串，在每个字符串的末尾加上当前数字字母表中的每一个数字。

先插入一个哨兵""，

[""]

查到 2 = "abc", 删除哨兵，加上a,b,c。

[a,b,c]

查到3 = def，删除a，加上ad,ae,af。

[ad,ae,af,b,c]

删除b，加上bd,be,bf。

[ad,ae,af,bd,be,bf,c]

删除c，加上cd,ce,cf。

[ad,ae,af,bd,be,bf,cd,ce,cf]

代码

public class Solution {
    public List<String> letterCombinations(String digits) {
        List<String> result = new ArrayList<>();
        if (digits == null || digits.length() == 0) { return result; }
        String[] letterPad = new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
        result.add("");
        for (int i = 0; i < digits.length(); i++) {
            int digit = digits.charAt(i)-'0';
            String letters = letterPad[digit];
            ListIterator<String> ite = result.listIterator();
            while (ite.hasNext()) {
                String old = ite.next();
                ite.remove();
                for (int j = 0; j < letters.length(); j++) {
                    ite.add(old + letters.charAt(j));
                }
            }
        }
        return result;
    }
}

也可以这样写

如果不用ListIterator，也可以用像下面这样while(ans.peek().length()==i)，只对特定元素做处理。这样做很sexy，但工作中不值得推荐。

public List<String> letterCombinations(String digits) {
    LinkedList<String> ans = new LinkedList<String>();
    String[] mapping = new String[] {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    ans.add("");
    for(int i =0; i<digits.length();i++){ // 这行非常帅
        int x = Character.getNumericValue(digits.charAt(i));
        while(ans.peek().length()==i){
            String t = ans.remove();
            for(char s : mapping[x].toCharArray())
                ans.add(t+s);
        }
    }
    return ans;
}

结果

phone-number-3

回溯算法，递归版

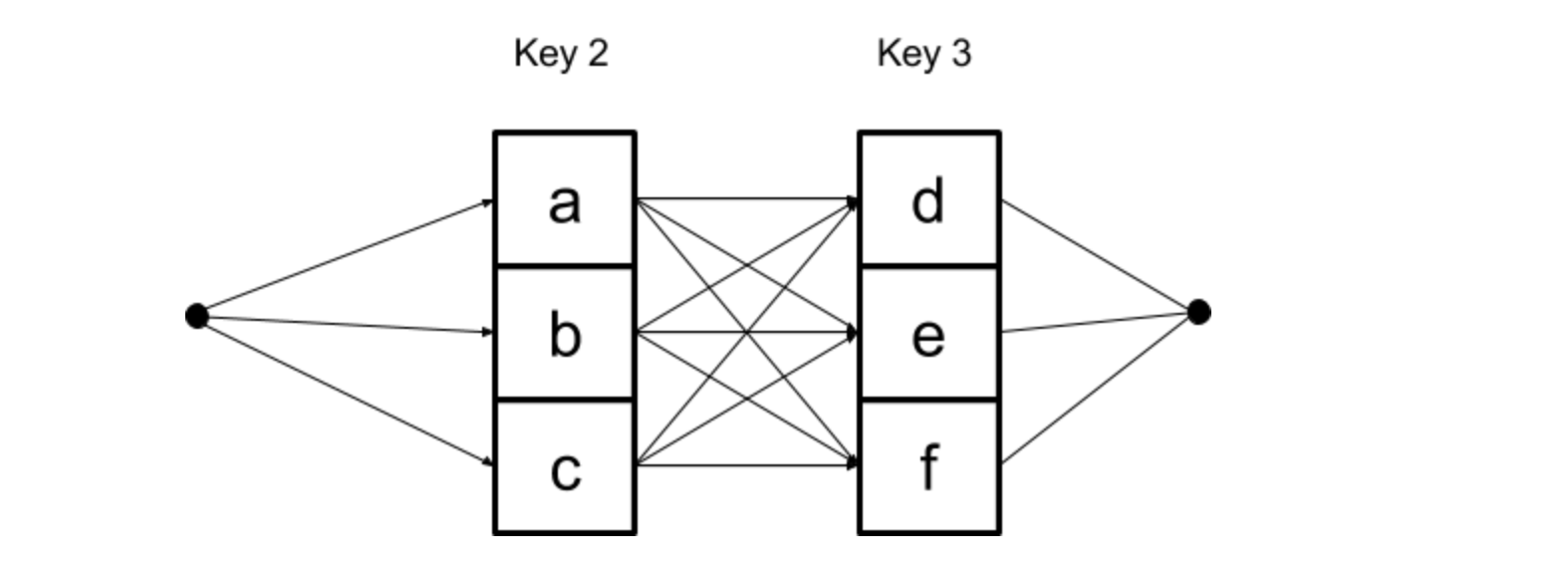
回溯算法用递归代码非常简洁，逻辑清晰。本质就是一个n叉树的动态规划问题。每当按下一个新的数字键，之前的任何一种可能，马上衍生出n种可能。用递归，就是每层都递归调用n次。 phone-number-dynamic

这里一个优化是，与其每次都更新List里的内容，不如最后写完了再放进List。

代码

public class Solution {
    public List<String> letterCombinations(String digits) {
        List<String> result = new ArrayList<>();
        if (digits.isEmpty()) { return result; }
        String[] letterPad = new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
        letterCombinationsRecursive(result,"",letterPad,0,digits);
        return result;
    }
    public void letterCombinationsRecursive(List<String> list, String str, String[] letterPad, int index, String digits) {
        if (index == digits.length()) { list.add(str); return; }
        for (char c : letterPad[digits.charAt(index)-'0'].toCharArray()) { // 当前按键上每个字母都是一条路
            letterCombinationsRecursive(list,str+c,letterPad,index+1,digits);
        }
    }
}

结果

phone-number-4