第一季 继电器
先不要扯什么图灵，冯诺依曼这些先贤。因为他们都太遥远。计算机一切计算的源头其实是源自一个非常非常中二的东西：“继电器（Relay）”。继电器是什么鬼？看下图，
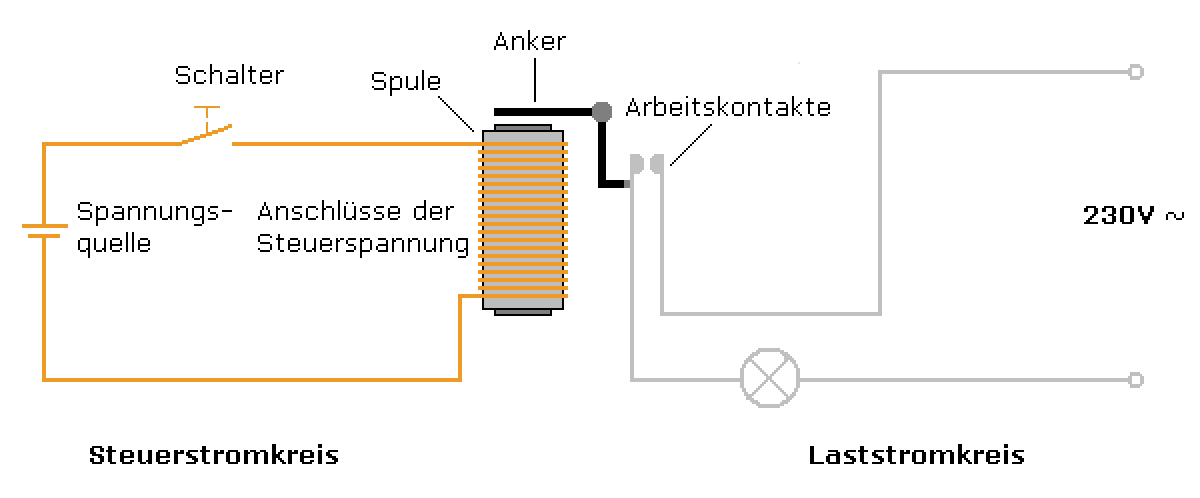其实就是一个线圈利用电磁感应做成的电磁铁。原理和“电报机”一样，当开关闭合，黄色电路通电，线圈是金属棒变成磁铁，吸引中间的小开关（Anker），接通右边灰色的电路，点亮灯泡。
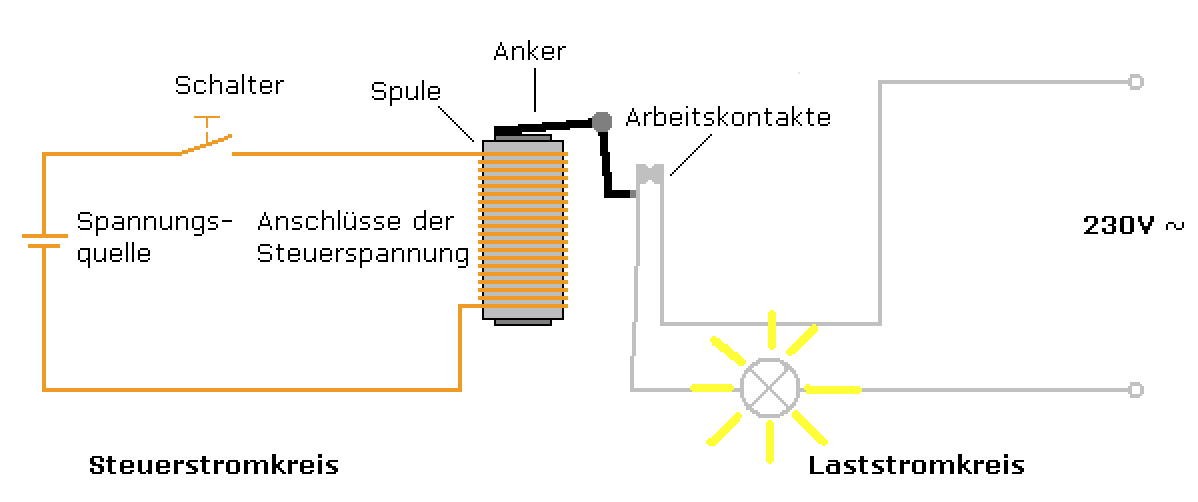简单说，就是你在家一按开关，隔壁老王家的灯亮了。
第二季 “反相器”和“非门”
为什么说继电器是个很中二的东西？因为这不就是开关吗？我按了它才亮，不按绝对不亮。但CPU真就是这货发展而来的。它的变种就开始好玩了。最简单的一个变种，就是“反继电器”，或者叫“反相器（Inverter）”。就是隔壁老王家的灯本来是亮着的，我手上的开关一按，灯就灭了。
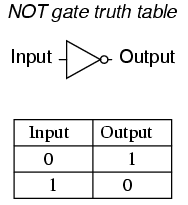
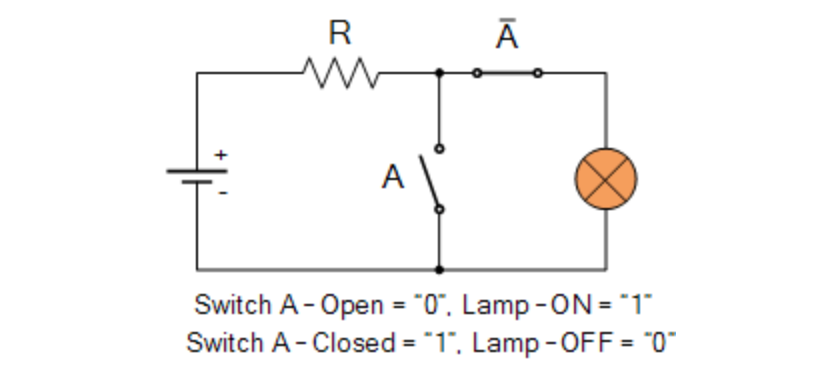“反相器”到了现代计算机里，就叫做“非门（NOT Gate）”。本来开关T1是接通的，Output是1（5V高位电平）。一旦闭合开关T1，电路中断，输出变为0（1V低位电平）。
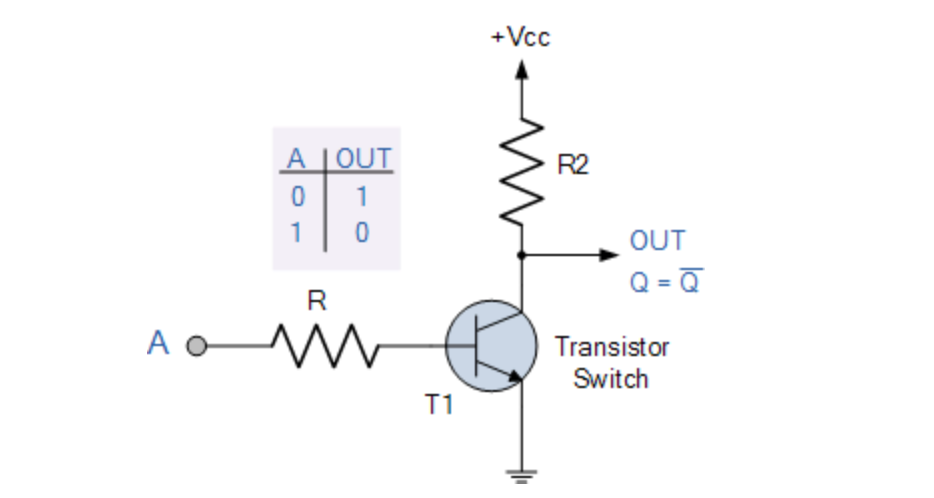“非门”用下面这个符号表示。简单说，就是输出永远和输入是反的，输入1，输出就是0。输入0，输出就是1。
第三季 逻辑门家族
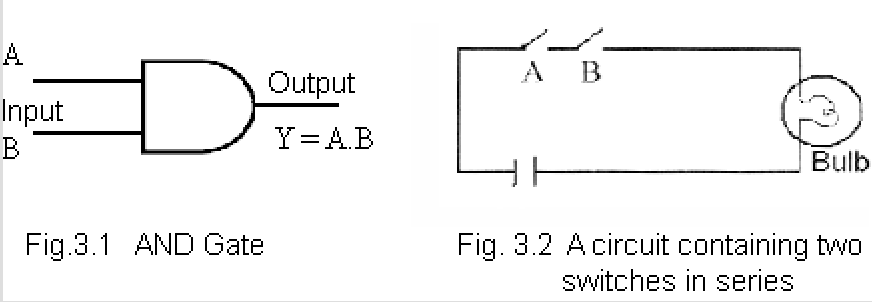
和“非门”一样，我们能得到一堆其他特性的门。比如，“与门（AND Gate）”，就是两个开关串联。必须两个开关同时闭合，灯泡才能亮。
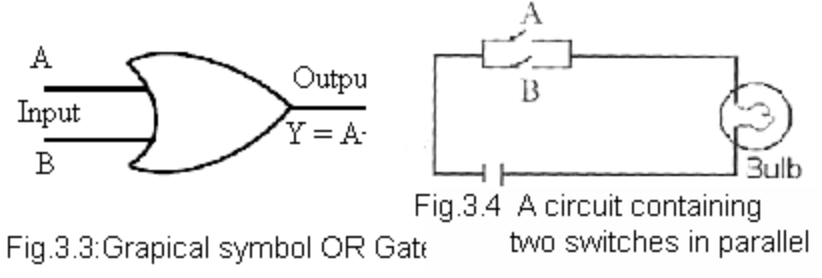
“或门（OR Gate）”，两个开关并联，只要其中一个开关闭合，灯泡就会亮。
长话短说，下图是所能得到的几个基本“逻辑门（Logic Gates）”。
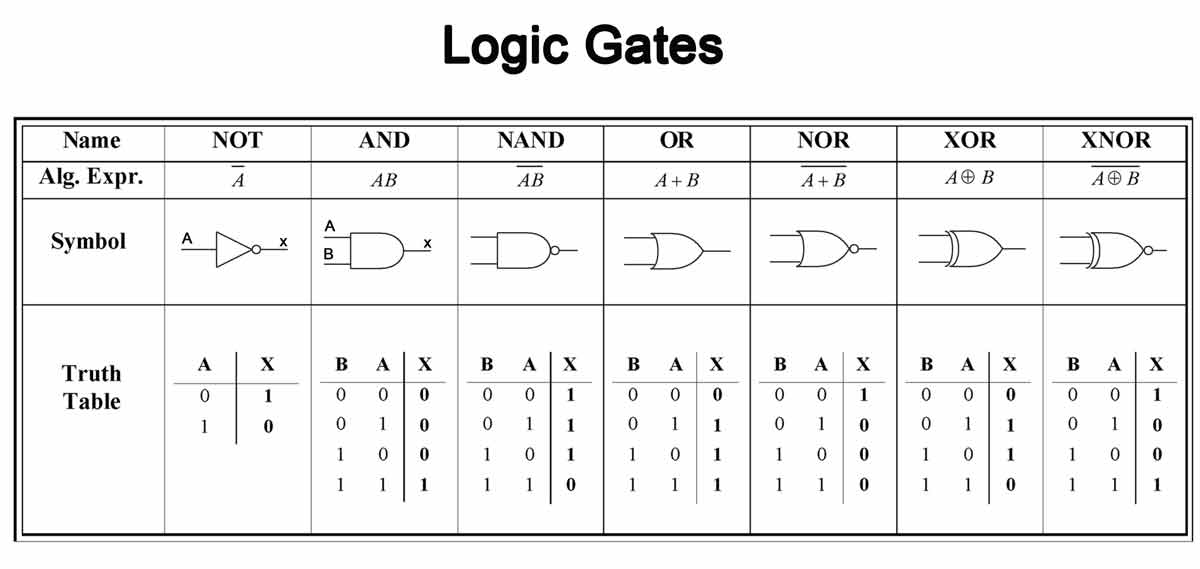
虽然看上去比较复杂，但“逻辑门”在本质上和之前讲的“继电器”都是“控制电路”。或者说都是我手里握着控制老王家花式吊灯的各种开关。老王一定很郁闷。
第四季 逻辑
逻辑门虽然被我说得很淳朴，就是控制隔壁老王家吊灯的开关。但其中却可能蕴含着人类大脑，甚至是这个世界终极奥义的一部分：逻辑（Logic）。这也是为什么它被叫做逻辑门。
爱因斯坦曾说过：
- 世界上最不可思议的事情,就是这个世界是可以被“理解”的。
简直是细思极恐有木有！最简单的例子，亚里士多德给出的经典“Barbara”三段论：
- 如果所有人（M）都是必死的（P），（大前提）
- 并且所有希腊人（S）都是人（M），（小前提）
- 那么所有希腊人（S）都是必死的（P）。（结论）
数学上，一个形式系統（Formal system）的野心就是想通过一组公理，和逻辑推理过程，来描述和证明我们的客观世界。说到这里我们计算机的祖师爷们就都出来了：莱布尼兹，康托尔，布尔，图灵，等等等等。著名的图灵机就是在这个议题的争论中无心插柳的副产品。这个主题无法展开。感兴趣推荐看 《逻辑的引擎》 这本书。这里只举一个最简单的 “布尔代数（Boolean algebra）” 的例子：
- 我喜欢（长头发）的（不是）（蛇精脸）的女生
用布尔代数来表示就是：
- 长头发 AND （ NOT 蛇精脸）
说到这里，是不是和前面说的逻辑门联系起来了？
第五季 逻辑电路
这里又要提到一位大师，克劳德·艾尔伍德·香农（Claude Elwood Shannon）和他的那篇史上最牛硕士论文：《继电器与开关电路的符号分析》。绝对最牛，没有之一！
还是之前那个例子：
- 我喜欢（长头发）的（不是）（蛇精脸）的女生
如果：
- A代表：长头发
- B代表：蛇精脸
那我喜欢的女生就可以写成一个布尔函数：
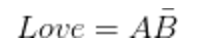
转换成“逻辑表决器”如下图。原理很简单，当A=1时，纵向的A总线为1。当A=0时，反A总线输出1。B也是如此。最后的输出线搭在A总线和反B总线上，用个与门连接。
所以只有当A的输入为1，B的输入为0时，Out才为1，代表我能接受这个女孩。不信大家可以人肉推演一下。
理论上任何布尔函数，都能转换成上面这样的表决器。就好像电路有了人类逻辑思考的能力。
第六季 “图灵机”和“累加器”
总算要说到计算机的祖师爷 图灵（Turing） 了。图灵机模型，相比上面说到的逻辑电路，要多一个“存储器”。根据图灵机模拟人类计算时大脑的工作状态的模型，人类计算加法也可以抽象成一个机械化的过程。
考虑5+7=12这个加法。5加7的结果是2，然后心中默记产生的一个进位。最终写成12。
5
+ 7
-----
12
换成二进制，是一个道理，
0000 0101
+ 0000 0111
-------------
0000 1100
其中每一位的加法还是能分解成两个动作：
- 同一位的两个数字相加
- 如果当前位结果大于1，则向前进一位
第一个动作可能的结果（真值表）有：
- 0 XOR 0=0
- 1 XOR 0=1
- 0 XOR 1=1
- 1 XOR 1=0
这个真值表和一个简单的“异或门”是一致的。
第二步进位，只有1+1才需要进位1，所以真值表如下：
- 0 AND 0=0
- 1 AND 0=0
- 0 AND 1=0
- 1 AND 1=1
这和“与门”的真值表是一致的。
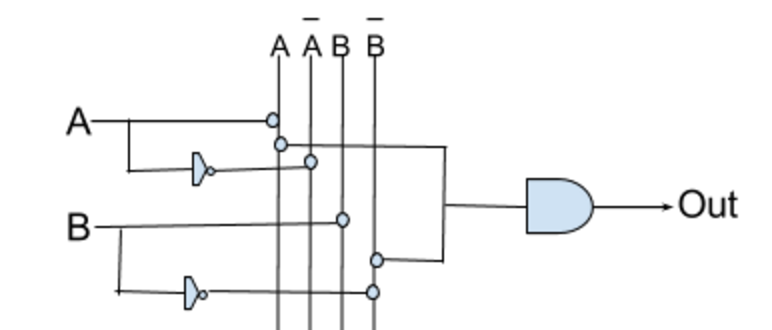
所以把一个“异或门”和一个“与门”组合到一起，就构成了一个“一位半加器”：
但事实上一位半加器只适用于末位数的加法。高位的二进制加法需要考虑3个输入，就是还需要额外考虑上一位得到的进位。这个过程可以用两个半加器来完成。
两个半加器组合起来，构成一个完整的“一位全加器”。
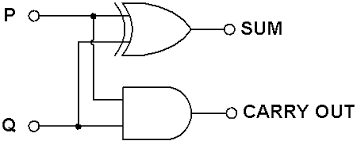
把8个这样的一位全加器组合起来，就构成了一个“八位全加器”：
从最末尾开始相加，刚才的5+7：
- 0000 0101 + 0000 0111
反过来就变成：
1010 0000
+ 1110 0000
-------------
0011 0000
把最初的进位c_in设为0，得到的结果反过来就是：0000 1100 = 12。
至此，计算机好像拥有了人脑的部分智能。既然一组逻辑门，能计算加法，就一定能做减法，乘法，除法，和其他计算。
第六季 寄存器
加减乘除远远不是逻辑门能做的全部事情。实际上电脑里出了硬盘，风扇，电池，其他几乎全是由逻辑电路和逻辑门组成的，包括我们说的内存。说内存先要说一下寄存器。这东西我觉得是比CPU更神奇的一个东西。绝对是一大黑魔法。用几个简单的逻辑门，就能在不断电的情况下一直”记住“上次的输入值。
最简单的储存部件叫“SR锁存器（Latch）”。其实就是两个“或非门”。
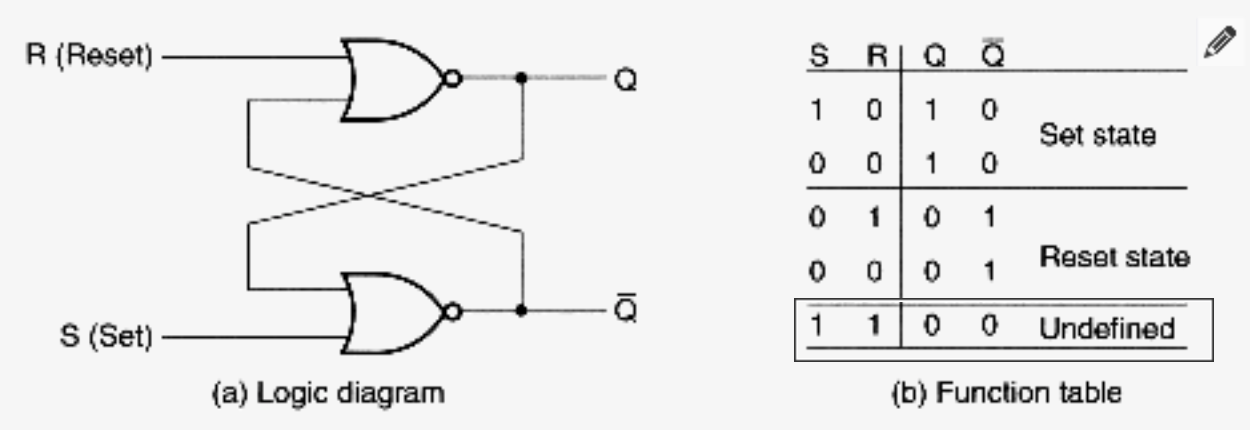再看一眼或非门的真值表：只有两个输入都为0，才输出1。
- 0 NOR 0 = 1
- 1 NOR 0 = 0
- 0 NOR 1 = 0
- 1 NOR 1 = 0
其中具体电流怎么通过互相博弈达到稳态的细节就不展开了。总之这个黑科技的最终效果就是：
- 假设初始状态都是零：S=0, R=0。输出Q=0，=0
- 当S端给个信号1，输出Q=1，=0
- 当S端变回信号0，输出还是保持Q=1，=0
也就是说，这个元件记住了之前S端的输入1。直到我们把R端设为1，输出Q才变回0。
虽然这个SR锁存器离我们真实的“RAM内存”还很遥远。但让逻辑门产生“记忆”的核心逻辑稳态锁就是这么简单的两个或非门。
当我们把SR锁存器的两个输入端捏合成一个D输入端，再加上一个由时钟信号控制端E，就得到一个更高级的“时序D锁存器”。如果不想头痛，只要记住这是一个能在时钟开关E打开的情况下，记住D输入端进来的信号的装置。之后我们一直可以从Q端得到之前D端的值。
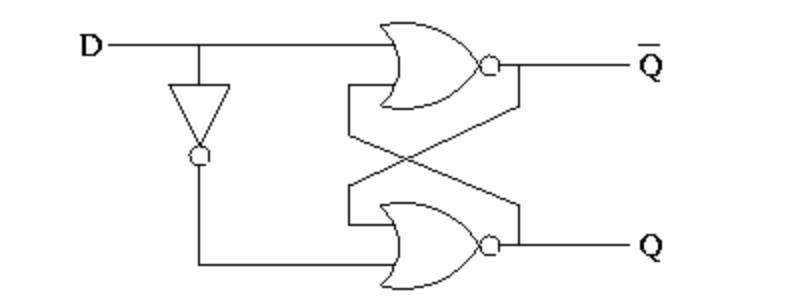
如果再复杂一点，把两个相反的时序D锁存器组合在一起，就能构成一个“D触发器（D Flip Flop）”：
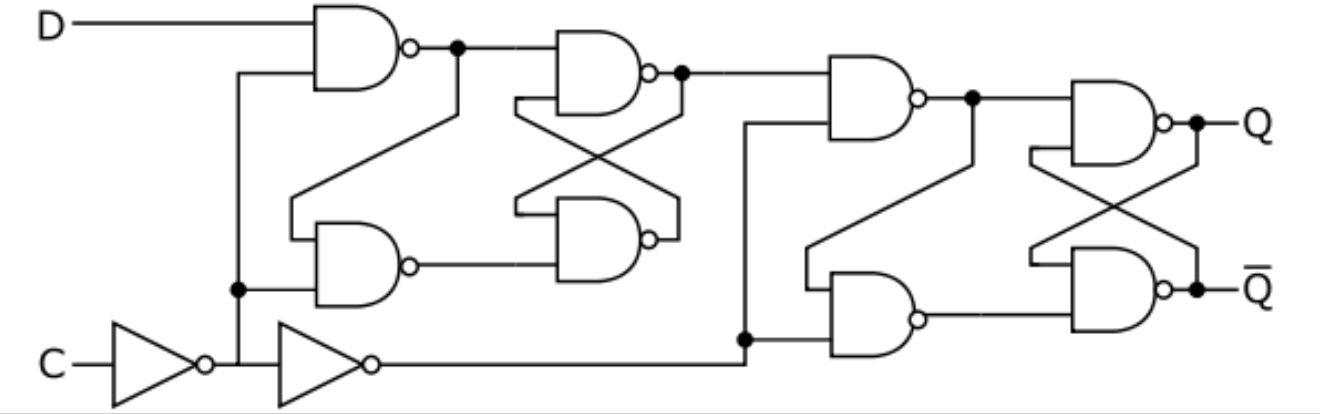触发器和之前的锁存器的区别是，只有当时钟信号处在上升沿（从1V向5V跃迁）的一瞬间，D端的输入值才能写入触发器。并在随后的时间内，只要没有新的D输入写入，Q一直保持这个值。
D触发器离我们的内存就没那么远了。只要再套上一个用于寻址的“解码器”和之前说过的“选择器”，就能实现从特定一组触发器中读取数据的效果啦。
所以我们都知道CPU需要时钟来同步时序电路。但这个晶振时钟并不是像想象的那样直接作用在ALU（逻辑运算单元）上，而是通过寄存器来实现时序控制。
第七季 硬件 V.s. 软件
虽然，几乎所有计算都能设计出一个专门的逻辑运算器。但这样做似乎并不明智，否则逻辑部件的数量将以指数级增长。一个合理的方案，应该是用硬件实现部分必须的基础计算功能，然后已软件的方式，利用基础计算单元，完成复杂计算。
就好像做乘法，不需要设计一个专门的“乘法器”，而是重复多次加法运算即可。这里就是所谓软件开始介入的地方。也就是所谓的“算法”开始放发挥作用，虽然并不是硬件无法胜任这项工作，而是把复杂性交给软件来处理似乎更合理。
从此，在硬件这棵树上，开出了软件这朵花。也就有了”程序员“这个严重伤害颈椎和腰椎的职业。