How int works in Java?

    |     java integer   |    

摘要

Java中的int使用 32位带符号2的补码

2的补码就是：每一对对应的正负数相加，正好进位。比如8 + (-8) = ?，写成二进制就是：00001000 + 10001000 = 100000000。

用2的补码的好处就是：使正负数的运算，可以和纯正数的加法使用同一套运算规则。

32-bit signed two’s complement integer

Java中int基本型，使用 32位带符号2的补码 来表示正负数。Oracle官方手册上的定义如下：

By default, the int data type is a 32-bit signed two’s complement integer, which has a minimum value of \(-2^{31}\) and a maximum value of \(2^{31}-1\).

直觉上，可能会觉得直接用最高位表示正负号，数字部分完全不变，这样更好理解。

+8 = 00001000
-8 = 10001000

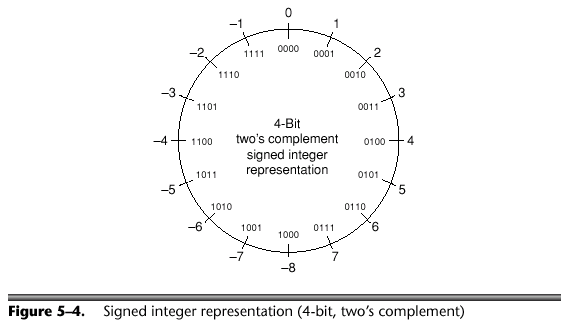
但2的补码不是这样表示负数。具体机制如下图， two-complement

把一个正数，转换成对应的负数，分两步走，

  1. 每一个二进制位都取相反值，0变成1，1变成0。
  2. 将上一步得到的值加1。
+8 = 00001000

第一步，取反：00001000 -> 11110111
第二步，加一：11110111 -> 11111000

-8 = 11111000

为什么一定要2的补码

下面这段，摘自阮一峰的网络日志，讲得非常好，http://www.ruanyifeng.com/blog/2009/08/twos_complement.html

首先，要明确一点。计算机内部用什么方式表示负数，其实是无所谓的。只要能够保持一一对应的关系，就可以用任意方式表示负数。所以，既然可以任意选择，那么理应选择一种最方便的方式。 2的补码就是最方便的方式。它的便利体现在，所有的加法运算可以使用同一种电路完成。

还是以-8作为例子。假定有两种表示方法。一种是直觉表示法，即10001000；另一种是2的补码表示法，即11111000。请问哪一种表示法在加法运算中更方便？

随便写一个计算式，16 + (-8) = ?。16的二进制表示是 00010000，所以用直觉表示法，加法就要写成：

　０００１００００
＋１０００１０００
－－－－－－－－－
　１００１１０００

可以看到，如果按照正常的加法规则，就会得到10011000的结果，转成十进制就是-24。显然，这是错误的答案。也就是说，

使用符合直觉的直接加正负号的表示法，正常的加法规则不适用于正数与负数的加法，因此必须制定两套运算规则，一套用于正数加正数，还有一套用于正数加负数。从电路上说，就是必须为加法运算做两种电路。

现在，再来看2的补码表示法。

　０００１００００
＋１１１１１０００
－－－－－－－－－
１００００１０００

可以看到，按照正常的加法规则，得到的结果是100001000。注意，这是一个9位的二进制数。我们已经假定这是一台8位机，因此最高的第9位是一个溢出位，会被自动舍去。所以，结果就变成了00001000，转成十进制正好是8，也就是16 + (-8) 的正确答案。这说明了，

2的补码表示法可以将加法运算规则，扩展到整个整数集，从而用一套电路就可以实现全部整数的加法。

2的补码的本质: 正负数相加

2的补码的本质，其实就是： 一对正负数，二进制加起来，正好进位。

１００００００００
－００００１０００   // +8
－－－－－－－－－
　１１１１１０００   // -8

进一步观察，可以发现100000000 = 11111111 + 1，所以上面的式子可以拆成两个：

　１１１１１１１１
－００００１０００
－－－－－－－－－
　１１１１０１１１
＋０００００００１
－－－－－－－－－
　１１１１１０００

2的补码的两个转换步骤就是这么来的。

参考文献

[1]阮一峰的网络日志 http://www.ruanyifeng.com/blog/2009/08/twos_complement.html